统计学中有很多概念很抽象不容易理解,但是如果有恰当的例子作桥梁,就可以深入浅出,容易让人领悟了。
最近尝试学习一些关于项目反映理论(IRT)的东西,觉得很多学习资料都使用公式吓唬人,并没有把这个概念浅显化和生活化。总之,这些资料不够友好,让初学者望而生畏。
那么什么是项目反映理论呢?我试着解释解释。这样从测量开始说起。举个例子,推铅球比赛。每个运动员都会按照规定选择一定大小的铅球站在指定的地点,用尽全力把球向着一个方向推出去。然后裁判会用尺子测量落地点与原点的距离,读出读数作为成绩。实际上测量的是选手的推力和推送技巧,它有一个理论的真值。而裁判的读数则是观测值。但是理论值并不等于观测值。理论值=观测值+误差。这就是经典的测量理论。但是铅球有不同重量和大小,假如在比赛记录中,有两个不同时期的运动员,一个用的是15斤,一个是10斤,前者推了15米,后者推出了20米,那么那个选手的成绩更好呢。这个时候经典测验理论就无能为力了,要解决这个问题必须要再把两个运动员找来,用同一个铅球重新比过。但是项目反映理论则可以解决这个问题。
实际上,教育测量往往比这个情境还要复杂。推铅球我们还能直接测量然后读数,即使有误差,多测几次就能减少误差。当是教育测量则通常是纸笔测验,这个题答对那个题每答对,最后有个总分。那么这个总分就是我们学生的学业能力吗?当然不是,比如这张试卷一共十个题目。有些简单题目很多人答对,有些难题则很少人答对。假如有两个学生都得了8分。一个学生把难题都做对了,但是简单题却错了两个。另外一个则是两个最难的题目都做错了。那么他们的学业能力真的一样吗?你觉得谁的学业能力应该更强一些?(想一想)
如何思考这个问题呢?我们还是用推铅球这个例子。由于某种原因,我们无法直接测量了,比如没有尺子并且是夜晚。那怎么比赛呢,于是我们选几个离河边远近不同的几个测试点,然后在每个点放一堆大小相同的铅球。虽然我们不能测量,但是我们仍然能区分铅球是否落水,听到落水声就得1分,否则0分。就好像做选择题,我们能判断是否选择了正确的选项。由于每个测试点离河边远近的距离都不同,铅球的大小也不同,而且河岸的形状也有变化,所以每个测试点的难度也不同。但是同一个选手在状态相同的情况下,测试结果理论上是相同的。我们将会根据每个测试点选手的表现来估计其能力水平。如果按照总分把所有选手分成高分组和低分组,对于同一个测试点,我们会发现高分组的通过率会高于低分组,如果从群体中随机选取一个选手的话,来自高分组的选手将会有更高的概率通过,而低分组的选手则通过率会比较低。如果我们以选手的能力为横坐标,以通过某个测试点的概率为纵轴,那么就得到下面的曲线。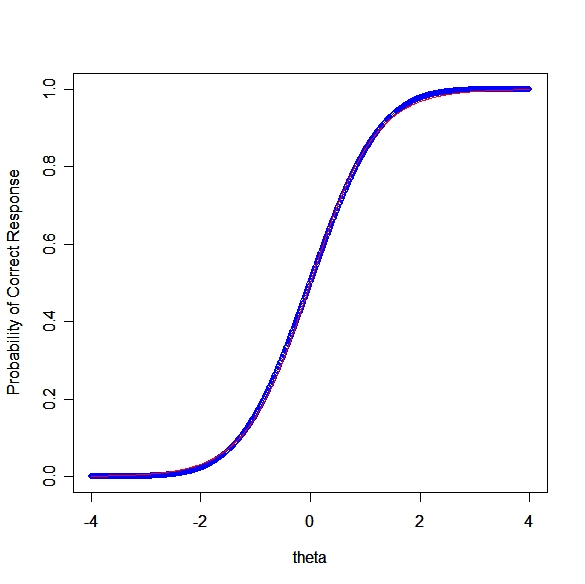
从这个项目特征曲线中我们可以看到,随着能力(theta)的提高,答对这个题目的概率也在提升。不同题目的曲线也不同,也许你已经想象出一道更简单题的题目的项目特征曲线将会相对这条曲线左移,而难题的曲线则右移。假如通过大量的测验知道了每个题目的项目特征曲线,那么我们就可以根据选手对一组题目的作答情况来估测其能力水平。即便是两个选手作答的两组试题并不相同,我们也能够比较两个选手的能力高低了。
当然项目特征曲线有简单的也有复杂的,简单1个参数(难度),也有2个(难度,区分度)或3个参数(难度,区分度和猜测参数)的,也就是所谓1P模型,2P,3P模型。
了解更多关于IRT的知识,请参考学习资料见:IRT learning resources - Chunlei’s Blog
为了更好解释项目反映理论,我曾经想过很多其他的例子,但是还是觉得推铅球这个例子最好,最能深入浅出,又不失去科学性。但是好的例子往往不是一下子就想到的,而且往往需要比较后才能选择出来,我以前想到的例子也列出来,读者可以自己比较比较。
A 抛硬币或者骰子
B 测量身高
C 摸高
D 跳高
比较的依据:
1 是否用来衡量某种能力
2 是否可测量,与经典测量理论相联系
3 群体的这种能力的分布是否为正态分布
4 是否能解决不同尺子测量结果比较的问题

