统计学比较抽象,需要通过例子加以学习。
比如第一型错误(Type I error)和第二型错误(Type II error)。比如验证一个人的智商是否超常(极高或者极低),我们知道95%人群的智商在70-130之间,一般成正态分布。我们会做出一个零假设H0,假定某人的智商是正常的。然后用某种评估方法测量一个人的智商结果是145,超出正常范围,这样我们就否定零假设,认为该人智商是超常的。
但是我们的评估方法不一定准确,所以不可避免的会犯错误。第一型错误是,该人智商属于正常范围(接受H0),但是的统计评测显示的却是超常(拒绝H0)。第二型错误是,该人智商明明超常(拒绝H0),结果我们统计评测显示该人智商正常(接受H0)。简单说也就是假阳性和假阴性,或者假检出和假包含。
分析数据就像是在森林里寻宝,每次进入森林都很不容易,需要花很多时间,非常容易迷失方向,面对无数的表格和无数的可能分析方法不知所措。而且好不容要到的路径,下次再想用却忘记了,需要花费很多实践才能再次找到。于是很多人做了很多无用的功,就是在原地打转。为了避免这样的情形发生,分析数据时一定要写分析记录和报告,否则即便是文件夹里有无数的报表,也忘记当初这个报表是干什么的了。
如何使用SPSS绘制重复测量的误差条图?答案是可以使用SPSS的graph builder,不过我在用的过程中发现一个很低级的错误。我搜索到了一个视频教程Create a clustered bar or line chart of means for repeated measures data (with optional error bars) on Vimeo。其实原理很简单,就是把多个变量同时拉到纵轴。但是我拉的时候,系统却不容许,也不报错。晕。后来发现,原来这些变量必须是scale类型,而不能是normal。全部粘贴覆盖为scale之后,问题解决。不提示为什么不能拖拽,这是SPSS设计上的缺陷。其实类似的问题还有,当你使用Multiple Imputation(MI)处理缺失数据的时候,如果变量类型不是scale,SPSS也会拒绝执行MI,这也是在网上查了才解决的。因此,在使用SPSS的时候一定要小心的变量类型,尽量最开始就设好。
下面进入正题,如何进行重复测量的方差检验。其实如何做并不难,难的是如何解释Spss产生的一大推报表,并选择有用的信息进行报告。首先这样的检测一般可以分为两类:One Way Anova以及Two-way Anova。前者是单因素实验设计,后者是双因素实验设计(如V1(2)× V2(3)交叉设计,共有6组)。两者的区别以后再解释。
此外还有组间变量(比如不同的处理、教学方法、培训类型)和协变量(性别、教育程度)等。
这种统计方法往往可以让你检测是否存在交叉效应。
在报告的时候,SPSS同时给你multivariate test和Univariate test的结果。到底报告那个呢?取决于Mauchly’s Test of Sphericity,如果sig<0.05那么,说明球度(sphericity)假设不成立,那么就要看修正后的Univerite test的结果。Spss提供多个修正结果,根据Epsilon-Greenhouse-Geisser的值是否大于0.75进行不同的选择,如果大于则选择Huynh-Feldt修正的结果,否则则选Greenhouse结果。
另外就是如何报告F检验的结果。通常报告的格式如下F(自由度,误差自由度)=F值,p=sig,n=total。这些值在哪里呢?看下图。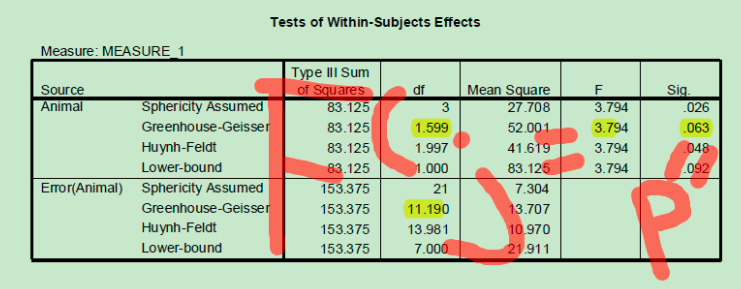
那么如何报告One way Anova的结果呢?
One way Anova
APA报告格式为:F(3,165)=2.836 p=0.04<.05
其中3为组间自由度(组数4-1),165为组内自由度(样本总数169-组数4)。所以看到这个结果,就知道共分4组,样本总量为169(3+165+1)。F值为2.836,p值为0.04,达到了显著水平。

